概要

jHitCylinder 関数は jHitSphere と同じように、3D空間中で光線が円柱によって遮られるか否かを判定します。

この関数は比較的稀にしか使われません。

jHitSphere や jHitBox と組み合わせて複雑な衝突形状を作るのに用いられます。

私は jHitSphere の原理を忘れてしまっていたので、今回は実装より先に書いておきます。

原理

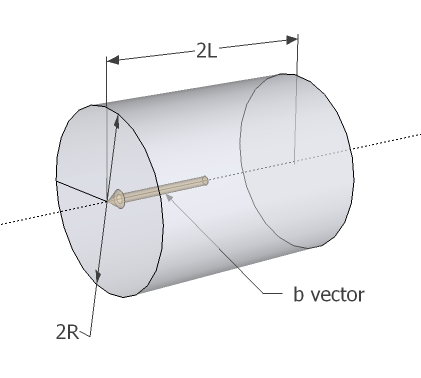
長さ $L$ の軸を表すベクトル $\vec{b}$ が与えられたとしましょう。このベクトルは円柱の軸を表し、円柱両端の平面の法線ベクトルにもなっています。ベクトルの長さは円柱の長さの半分を表します。

円柱の半径は $R$ であらわされます。

下図はこれらの変数を説明するものです。

$2R$ は直径を表し、 $2L$ は円柱の長さを表すことに注意してください。

円柱の寸法

光線と円柱両端の平面との交点の解法

最初に得られるのは平面のベクトル方程式での表現です。

$(\vec{r} \pm \vec{b}) \cdot \vec{b} = 0$

それから光線のベクトル方程式もわかります。

$\vec{r}=\vec{a}+t\vec{d}$

$\vec{r}$ を代入することによって次の式が得られます。

$(\vec{a} + t\vec{d} \pm \vec{b}) \cdot \vec{b} = 0$

この式は $t$ に関して下式のように解くことができます。

$t = \frac{(\vec{a} \pm \vec{b}) \cdot \vec{b}}{\vec{d} \cdot \vec{b}}$

この $t$ を光線のベクトル方程式に代入することによって、平面と光線の交点が求まります。したがって、交点と円柱の軸との距離を求めることでヒットしたかどうかを判定することができます。

光線と円柱の側面との交点の解法

円柱の側面の解きかたは球の場合とよく似ています。光線を円柱の軸と垂直な平面に投影し、 jHitSphere と同じことをするだけです。

最初に、円柱の軸を正規化したベクトルを $\hat{b} \equiv \vec{b}/\vert \vec{b}\vert $ と定義します。

円柱の軸に垂直な平面に投影したベクトルをいくつか作りましょう。

$\vec{r_0'} \equiv \vec{r_0} - (\vec{r_0} \cdot \hat{b}) \hat{b}$ $\vec{d'} \equiv \vec{d} - (\vec{d} \cdot \hat{b}) \hat{b}$

jHitSphere と同じ理屈で次の解が得られます。

$t=\frac{-\vec{r_0'}\cdot\vec{d'}\pm\sqrt{(\vec{r_0'}\cdot\vec{d'})^2-\vert \vec{d'}\vert ^2(\vert \vec{r_0'}\vert ^2-R^2)}}{\vert \vec{d'}\vert ^2}$

この $t$ を光線のベクトル方程式に代入し、軸方向の距離を測ることによって、この $t$ が円柱との交点を示しているかどうかを知ることができます。

また、この解の判別式

$D=(\vec{r_0'}\cdot\vec{d'})^2-\vert \vec{d'}\vert ^2(\vert \vec{r_0'}\vert ^2-R^2)$

が 0 より小さい場合は、円柱両端の面に対してすら、交差は生じません。というのも、無限に延長した円柱と光線の間にはねじれの位置のような関係があるからです。

これって車輪の再発明じゃないの？

こういう場合、普段は外部のライブラリを使うべきです。というのも外部のライブラリはお手製のアルゴリズムよりもテストされ頑健であるのが普通だからです。

我々はすでに直方体や球や円柱だけでなく任意の凸形ポリゴンをサポートする Bullet dynamics engine の光線テストアルゴリズムを手にしています。 Bullet の問題は、理由は不明なのですが、弾丸と物体の当たりを判定する用途には信頼性がないということです。衝突マージンとの関係があるのかもしれませんが、 Bullet dynamics engine の奥深くまで追求しいていないので確かなことは言えません。